
Cómo calcular la desviación estándar

Curiosamente, en el mundo real, ningún estadístico calcularía la desviación estándar a mano. Los cálculos involucrados son un poco complejos y el riesgo de cometer un error es alto. Además, calcular a mano es lento. Muy lento.
Por eso, los estadísticos confían en hojas de cálculo y programas de computadora para procesar sus números.
Entonces, ¿cuál es el punto de este artículo? ¿Por qué dedicamos tiempo a aprender un proceso que los estadísticos no usan en realidad?
La respuesta es que aprender a hacer los cálculos a mano nos dará una idea de cómo realmente funciona la desviación estándar. Esta comprensión es valiosa.
En lugar de ver la desviación estándar como un número mágico que nos da nuestra hoja de cálculo o programa de computadora, seremos capaces de explicar de dónde proviene ese número.
¿Qué es la desviación estándar?
La desviación estándar es una medida que indica cuánto se desvían (se dispersan) los valores del conjunto de datos de la media. Dicho de otra manera, la desviación estándar muestra si tus datos están cerca de la media o si fluctúan mucho.
El propósito de la desviación estándar es ayudarte a comprender si la media realmente devuelve un dato "típico". Cuanto más cercana a cero sea la desviación estándar, menor será la variabilidad de los datos y más confiable será la media.
Una desviación estándar igual a 0 indica que cada valor en el conjunto de datos es exactamente igual a la media. Cuanto mayor sea la desviación estándar, mayor será la variación en los datos y menos precisa será la media.
Desviación de la muestra vs. desviación de la población
En relación con la desviación estándar, a menudo escucharás los términos "muestra" y "población", que se refieren a la completitud de los datos con los que estás trabajando. La principal diferencia es la siguiente:
- Población incluye todos los elementos de un conjunto de datos.
- Muestra es un subconjunto de datos que incluye uno o más elementos de la población.
Los investigadores y analistas operan con la desviación estándar de una muestra y una población en diferentes situaciones.
Por ejemplo, al resumir las calificaciones de un examen de una clase de estudiantes, un profesor utilizará la desviación de la población.
Los estadísticos que calculan la puntuación media nacional del SAT utilizarían una desviación estándar de la muestra porque solo se les presentan los datos de una muestra, no de toda la población.
Resumen de cómo calcular la desviación estándar
La fórmula para la desviación estándar (SD) es:
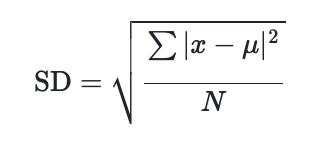
Donde:
- Σ significa "suma de"
- x es un valor en el conjunto de datos
- μ es la media del conjunto de datos
- N es el número de puntos de datos en la población.
La fórmula de la desviación estándar puede parecer confusa, pero tendrá sentido después de que la desglosemos. En las próximas secciones, recorreremos un ejemplo interactivo paso a paso.
Aquí tienes un pequeño adelanto de los pasos que vamos a seguir:
- Paso 1: Encuentra la media.
- Paso 2: Para cada punto de datos, encuentra el cuadrado de su distancia a la media.
- Paso 3: Suma los valores del Paso 2.
- Paso 4: Divide entre el número de puntos de datos.
- Paso 5: Calcula la raíz cuadrada.
Calculando la desviación paso a paso
Aquí te presento cómo calcular la desviación estándar paso a paso, con un enfoque amigable:
1. Encuentra la media (promedio) de tus datos:
- Suma todos los valores de tu conjunto de datos.
- Divide la suma total entre el número de valores en el conjunto de datos.
Ejemplo:
Si tu conjunto de datos es: 2, 4, 6, 8, 10
- La suma total es 2 + 4 + 6 + 8 + 10 = 30
- El número de valores es 5.
- La media es 30 / 5 = 6
2. Calcula la desviación de cada valor de la media:
- Resta la media de cada valor individual.
- Eleva al cuadrado cada resultado.
Ejemplo:
- Valor 1: 2 - 6 = -4, (-4)^2 = 16
- Valor 2: 4 - 6 = -2, (-2)^2 = 4
- Valor 3: 6 - 6 = 0, (0)^2 = 0
- Valor 4: 8 - 6 = 2, (2)^2 = 4
- Valor 5: 10 - 6 = 4, (4)^2 = 16
3. Encuentra la suma de las desviaciones cuadradas:
- Suma todos los resultados obtenidos en el paso 2.
Ejemplo:
- La suma de las desviaciones cuadradas es 16 + 4 + 0 + 4 + 16 = 40
4. Calcula la varianza:
- Divide la suma de las desviaciones cuadradas por el número de valores en el conjunto de datos menos 1.
Ejemplo:
- La varianza es 40 / (5 - 1) = 10
5. Calcula la desviación estándar:
- Obtén la raíz cuadrada de la varianza.
Ejemplo:
- La desviación estándar es la raíz cuadrada de 10, que es aproximadamente 3.16.
En resumen, la desviación estándar nos dice qué tan dispersos están los datos alrededor de la media. Una desviación más alta significa que los datos están más dispersos, mientras que una desviación estándar más baja indica que los datos están más agrupados alrededor de la media.
Aplicaciones de la Desviación Estándar
La desviación estándar se usa ampliamente en entornos experimentales e industriales para probar modelos contra datos del mundo real.
Un ejemplo de esto en aplicaciones industriales es el control de calidad para algunos productos. La desviación se puede utilizar para calcular un valor mínimo y máximo dentro del cual algún aspecto del producto debe caer un alto porcentaje del tiempo.
En los casos en que los valores caen fuera del rango calculado, puede ser necesario realizar cambios en el proceso de producción para garantizar el control de calidad.
La desviación estándar también se utiliza en el clima para determinar las diferencias en el clima regional. Imagina dos ciudades, una en la costa y otra en el interior, que tienen la misma temperatura media de 23.9°C (75°F).
Si bien esto puede llevar a creer que las temperaturas de estas dos ciudades son prácticamente las mismas, la realidad podría estar enmascarada si solo se considera la media y se ignora la desviación estándar.
Las ciudades costeras tienden a tener temperaturas mucho más estables debido a la regulación por grandes masas de agua, ya que el agua tiene una mayor capacidad calorífica que la tierra; esencialmente, esto hace que el agua sea mucho menos susceptible a los cambios de temperatura, y las zonas costeras se mantienen más cálidas en invierno y más frescas en verano debido a la cantidad de energía necesaria para cambiar la temperatura del agua.
Por lo tanto, mientras que la ciudad costera puede tener rangos de temperatura entre 15.6°C (60°F) y 29.4°C (85°F) durante un período de tiempo determinado para resultar en una media de 23.9°C (75°F), una ciudad del interior podría tener temperaturas que van de -1.1°C (30°F) a 43.3°C (110°F) para resultar en la misma media.
Otra área en la que la desviación estándar se utiliza ampliamente son las finanzas, donde a menudo se utiliza para medir el riesgo asociado a las fluctuaciones de precios de algún activo o cartera de activos. El uso de la desviación en estos casos proporciona una estimación de la incertidumbre de los rendimientos futuros de una determinada inversión.
Por ejemplo, al comparar la acción A que tiene un rendimiento promedio del 7% con una desviación estándar del 10% contra la acción B, que tiene el mismo rendimiento promedio pero una desviación estándar del 50%, la primera acción sería claramente la opción más segura, ya que la desviación de la acción B es significativamente mayor, para el mismo rendimiento exacto.
Eso no quiere decir que la acción A sea definitivamente una mejor opción de inversión en este escenario, ya que la desviación estándar puede distorsionar la media en ambas direcciones.
Si bien la acción A tiene una mayor probabilidad de un rendimiento promedio más cercano al 7%, la acción B puede proporcionar potencialmente un rendimiento (o pérdida) significativamente mayor.
Estos son solo algunos ejemplos de cómo se puede utilizar la desviación, pero existen muchos más. En general, el cálculo de la desviación es valioso siempre que se desee saber qué tan lejos de la media puede estar un valor típico de una distribución.
Referencias
La idea de la dispersión y la desviación estándar (artículo)
https://es.khanacademy.org/math/probability/data-distributions-a1/summarizing-spread-distributions/a/introduction-to-standard-deviation
Desviación típica - Entiende qué es de una vez por todas
https://economipedia.com/definiciones/desviacion-tipica.html
¿Quieres conocer otros artículos parecidos a Cómo calcular la desviación estándar?
Ya los puedes visitar la categoría Matemáticas.





