La Ley de los Signos Matemáticos
La ley de los Signos Matemáticos es un principio matemático que dicta cómo se combinan los signos de los números en las operaciones.
En la multiplicación o división de números con signos diferentes, el resultado es negativo. Por el contrario, si ambos números tienen el mismo signo, el resultado es positivo.
En la suma y resta, los signos se combinan según las reglas de la aritmética convencional.
Esta regla es fundamental para realizar operaciones con números enteros y expresiones algebraicas, lo que facilita la solución de problemas matemáticos.
Conjunto de leyes que gobiernan las operaciones básicas con números reales.
Propiedades de la Ley de los Signos Matemáticos
La suma de números reales se realiza de acuerdo con las siguientes reglas, donde a y b son números positivos:
- (+a) + (+b) = (a + b)
- (+a) + (–b) = (a – b) si a ≥ b y
(+a) + (–b) = –(b – a) si a < b - (–a) + (–b) = –(a + b)
- (–a) + (+b) = –(a – b) si a ≥ b y
(–a) + (+b) = (b – a) si a < b
La resta de números reales se realiza de acuerdo con las siguientes reglas, donde a y b son números positivos:
- (+a) – (–b) = (a + b)
- (+a) – (+b) = (a – b) si a > b y
(+a) – (+b) = –(b – a) si a < b - (–a) – (+b) = –(a + b)
- (–a) – (–b) = –(a – b) si a > b y
(–a) – (–b) = (b – a) si a < b
La multiplicación de dos números reales se realiza de acuerdo con las siguientes reglas:
- (+a) × (–b) = (–a) × (+b) = –ab
- (+a) × (+b) = (–a) × (–b) = ab
La división de dos números reales se realiza de acuerdo con las siguientes reglas:
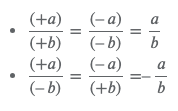
Los Signos Matemáticos
Símbolo de Suma (+)
El símbolo de suma (+) significa adición. Es el símbolo matemático más básico del mundo. Al sumar dos o más números, utiliza el símbolo de suma para indicar que los estás combinando. Por ejemplo, 6 + 3 significa que estás sumando el número positivo 6 y el número positivo 3 juntos. También puedes incluir el símbolo de suma antes de un número para indicar que el número es positivo, aunque esto suele ser redundante — se asume que un número por sí solo es positivo. Sin embargo, escribir "+3" es una forma de dejar claro que te refieres al 3 positivo.
Símbolo de Resta (-)
El símbolo de resta (-) significa sustracción. Cuando restas un número de otro, coloca el signo de resta entre ellos. Por ejemplo, 6 - 3 muestra que estás restando 3 de 6. Al igual que con el símbolo de suma, puedes colocar el símbolo de resta delante de un número para mostrar que tiene un valor negativo. Esto es mucho más común, ya que los números escritos no son negativos por defecto. Por ejemplo, escribir "-3" muestra que te refieres al 3 negativo.
Símbolo de Igualdad (=)
El símbolo de igualdad (=) indica que los valores a ambos lados del símbolo no son aproximadamente iguales, sino completamente equivalentes. En la ecuación 6 + 3 = 9, el signo de igualdad indica que la suma de 6 y 3 es equivalente a 9. El símbolo de igualdad es una parte esencial de cualquier ecuación matemática.
Símbolo de Desigualdad (≠)
El símbolo de desigualdad (≠) indica que dos valores no son iguales. Coloca este signo entre dos números o expresiones matemáticas que no son equivalentes. Por ejemplo, 6 ≠ 3 indica que 6 no es igual a 3.
Símbolo de Multiplicación (×)
El símbolo de multiplicación (×) significa multiplicar algo por otra cosa — es decir, encontrar el producto de dos números o, dicho de otro modo, sumar un número a sí mismo una cierta cantidad de veces. Dejemos esto claro con un ejemplo: 6 × 3 = 18 significa que estás sumando tres veces el 6, resultando en un producto de 18. Dado que el símbolo formal de multiplicación (×) no es común en los teclados, puedes usar un asterisco (*) o una "x" en su lugar. Esto es particularmente útil al escribir programas informáticos o fórmulas en Excel.
Símbolo de División (÷)
El símbolo de división (÷) significa dividir un número. Este es el proceso de dividir un número en una cierta cantidad de partes iguales. Considera la ecuación 6 ÷ 3 = 2. En este ejemplo, 6 se divide en 3 grupos iguales de 2. Al igual que el símbolo de multiplicación, el símbolo formal de división (÷) es poco común en el uso diario. Al escribir ecuaciones, puedes usar una barra inclinada (/) para indicar división. Nuevamente, esto es necesario para escribir ecuaciones en lenguajes de programación informática.
Símbolos de Mayor Que/Menor Que (> <)
El símbolo de mayor que (>) y el símbolo de menor que (<) no tienen el mismo significado, pero indican que un valor es mayor que otro. Estos símbolos funcionan de manera similar al símbolo de igualdad entre dos números. Por ejemplo, 6 > 3 muestra que 6 es mayor que 3, mientras que 3 < 6 muestra que 3 es menor que 6. Recuerda, el número más grande siempre enfrenta el extremo abierto del símbolo, mientras que el número más pequeño siempre enfrenta el punto donde se encuentran las dos líneas.
Símbolos de Mayor o Igual/Menor o Igual (≥ ≤)
El símbolo de mayor o igual que (≥) y el símbolo de menor o igual que (≤) combinan los símbolos de mayor que y menor que con el símbolo de igualdad. Se utilizan para, lo adivinaste, mostrar cuando dos valores son mayores (o menores) o iguales entre sí. Este símbolo no es muy común en el uso diario y es más prevalente en ecuaciones cuando una o más cantidades son desconocidas. Por ejemplo, en la ecuación X ≥ 3, sabemos que X puede ser 3 o cualquier número mayor que 3. En este caso, 3 ≥ 3 es una afirmación verdadera, al igual que 4 ≥ 3, 5 ≥ 3, y así sucesivamente.
Símbolo de Fracción (/)
El símbolo de fracción (/) aparece como una línea o barra que separa dos números, uno debajo del otro. Puede aparecer de diferentes maneras. Por ejemplo, 3/5 significa tres quintos. El 3 en la parte superior de la fracción está en la posición de numerador, y el 5 en la parte inferior de la fracción está en la posición de denominador. Las fracciones te muestran cuántas partes de un todo tienes; decir que tienes 3/5 de una galleta significa que, si una galleta se divide en cinco partes iguales, tienes 3 de esas partes. Para expresiones matemáticas más complicadas, el símbolo de fracción aparece como una larga línea horizontal que separa el numerador y el denominador.
Símbolo Decimal (.)
Un símbolo decimal (.) es un punto utilizado para separar la parte entera de un número de la parte fraccionaria de un número. Si eso suena un poco confuso, demos un paso atrás para entenderlo. El sistema numérico se basa en un sistema de valor posicional, lo que significa que la ubicación de cada dígito dentro de un número indica su valor. En el número 3.6, la ubicación del 3 indica que es la parte entera del número; el 6 está a la derecha del punto decimal en lo que llamamos el "lugar de las décimas," lo que significa que es 6/10 de 1. Si tuvieras 3.6 galletas, tendrías 3 galletas enteras y 6/10 de una galleta total. Los dígitos adicionales después del decimal tienen su propio valor posicional. En el número 3.687, el 8 está en el lugar de las centésimas y el 7 está en el lugar de las milésimas.
Símbolo de Porcentaje (%)
Al igual que el símbolo de fracción y el decimal, el símbolo de porcentaje (%) es uno de los objetos matemáticos clave, útil para mostrar cantidades fraccionarias, en este caso específicamente como una porción de 100. Si tienes 36% de la batería de tu teléfono celular, tienes 36 de 100 unidades de vida de la batería restantes. "Porcentaje" significa "de cien," y dado que el símbolo de porcentaje (%) parece los dígitos de 100 reorganizados, es fácil de recordar.
Ley de los signos matemáticos
Las ecuaciones matemáticas a menudo pueden parecer una masa confusa de garabatos aleatorios, pero todas están compuestas de símbolos matemáticos comunes, los los signos matemáticos.
La ley de los Signos Matemáticos nos proporciona las pautas necesarias para determinar el signo de un resultado al realizar operaciones con números reales. De manera general, a los números positivos se les puede incluir o no el símbolo «+».
Ley de los signos en la suma
Al efectuar sumas con números reales, se aplican las siguientes normas:
- Si ambos números son positivos (mayores que cero), se suman y conservan el signo «+».
- Si ambos números son negativos (menores que cero), se suman y el resultado mantiene el signo «-».
- Si se suma un número positivo y uno negativo, se restan y el resultado adopta el signo del número con mayor valor absoluto.
Ley de los signos en la resta
En las operaciones de resta con números reales, el signo de resta afecta al número que le sigue. Es decir, el signo del número cambia de acuerdo con la operación realizada.
Ley de los signos en la multiplicación
Cuando se multiplican números reales, el signo del resultado se determina según las siguientes reglas:
- Al multiplicar dos números positivos, el resultado será positivo.
- Al multiplicar dos números negativos, el resultado también será positivo.
- Si se multiplica un número positivo y uno negativo, el resultado será negativo.
Ley de los signos en la división
En las divisiones entre números reales, el signo del resultado sigue las mismas pautas que en la multiplicación:
- Si ambos números son positivos, el resultado será positivo.
- Si ambos números son negativos, el resultado también será positivo.
- Si uno de los números es positivo y el otro es negativo, el resultado será negativo.
¿Quieres conocer otros artículos parecidos a La Ley de los Signos Matemáticos?
Ya los puedes visitar la categoría Matemáticas.